Straightening a (360-degree) Panorama

( Deutsche Version aufrufen)
 

To work with this Tutorial, you need PTGui, Hugin or another Panotools-based Software. This Tutorial has been written with PTGui (Ver. 6)

It doesn't matter, which Software you are using - the basic workflow stays the same. Also, the GUI of PTGui and Hugin works in a similar way. It is only important that you understand the control point types that are used by the "Panorama Tools Optimizer" (PToptimizer): t0 (default), t1 (vertical) und t2 (horizontal)

The solution method: Vertical Control Points

Why vertical control points?

While normal ("t0") control points are used to correctly connect the source images, the types "t1" and "t2" are meant to align images and panoramas. But only one of these types can be used universally - the vertical! Horizontal control points are only valid for rectlinear projections, and in all projections for the definition of the horizon itself!

• To get the point: Lens types and output projections

  The definition of control points are always meant for the output projection!
  The lens type is the input projection. In the most simple case, you may work with an normal rectlinear lens. But this may not be always the case:

  lens type: circular fisheye (8 mm)
  output projection (corrected)	"rectlinear": note: maximum horizontal and vertical field of view may not exceed 120 degrees
  	"cylindrical": note: maximum vertical field of view may not exceed 120 degrees
  	"equirectangular":

  
  As you can see in the above example, there are only a few situations where you can rely that a straight line will always stay a straight line. Only verticals are always straight in the output, so we will use them as a "least common denominator".
   

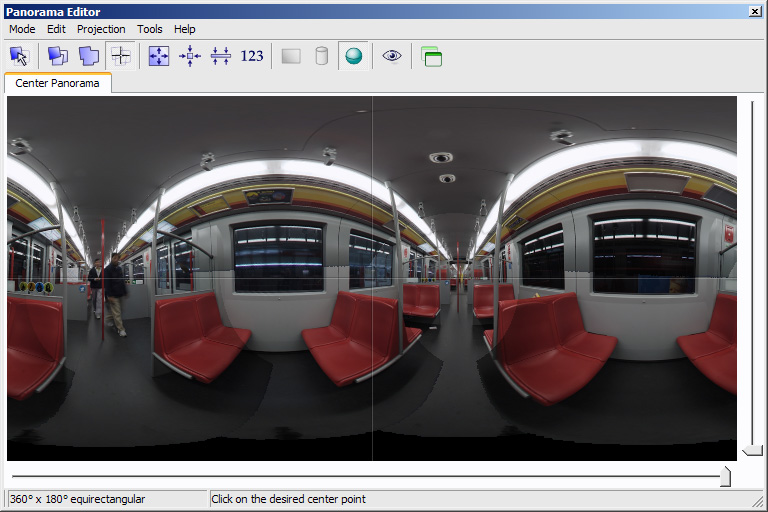
• The Realization: Setting the control points

  I assume, you are already familiar with the process of setting normal control points: One marks the same image feature in two (overlapping) images. The optimizer will then try to reduce the sum of control point distances until this sum is as small as possible.
  Setting a line is a little different: You don't use two overlapping images, you use the same image. And you don't mark the same image feature, but you set the control point along a straight (vertical) line.

  Unfortunately, this vertical line will only rotate the image, it won't align this image vertically. For this reason, we have to assign more vertical lines - best: one in every source image. For mathematical/geometrical reasons, this will not only rotate but also move the image into the correct vertical position - setting the horizon at the correct level.

  We will now do this with a practical example. Like always, you can download the source images here. If you have no practical experience in creating a 360-degree panorama, i suggest reading this article first.
  Here, we will continue at the point, where the source images are already loaded, the normal/standard control points set and optimized:

  
  (In this example, i've enhanced the horizon mis-alignment a little - meanwhile PTGui is pretty good in automatic alignment...)

  Before we start setting the vertical ("t1) control points, i want to point out a specific characteristic of this particular panorama. Although it may not be noticeable - not all verticals are really verticals. This is because the endwalls of the metro waggon are in reality slightly tilted. Though - even slightly tilted lines are in practice better than no verticals at all.

  I like to compare the behaviour of control points with a "lever force". When optimizing, all control points will correlate in a way that the sum of control point errors will be as low as possible. This simple rule can be used to priorize the vertical control points:
  If you are unsure if a line is really vertical, you can use only a small section of your vertical line. If you are pretty sure: use a larger section of your vertical line.

  We will now begin to set the first vertical control point: Switch to the "control point"-tab and select the same source image in both windows. You will notice that PTGui will automaticalls set the type to "t1" (vertical line):

  

  You can see a grab pole in the middle of the picture. We can safely assume the this pole is built as an exact vertical. So we can use the complete pole for assigning the control point:

  

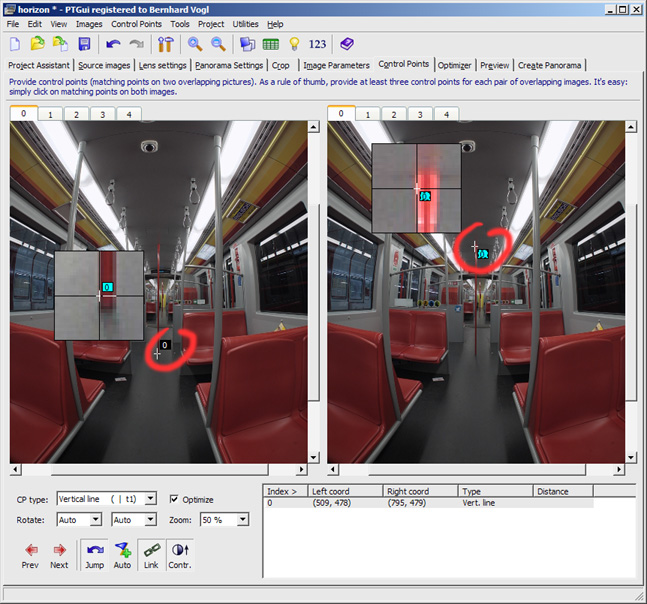
  We are now ready with the first picture. Click on the red "Next"-Arrow to switch to the next source image.
  
  Here we have the problem that we can't be sure that the lines are really vertical, but we can assume that they are approximately vertical. So we limit the control point to a smaller section:
  
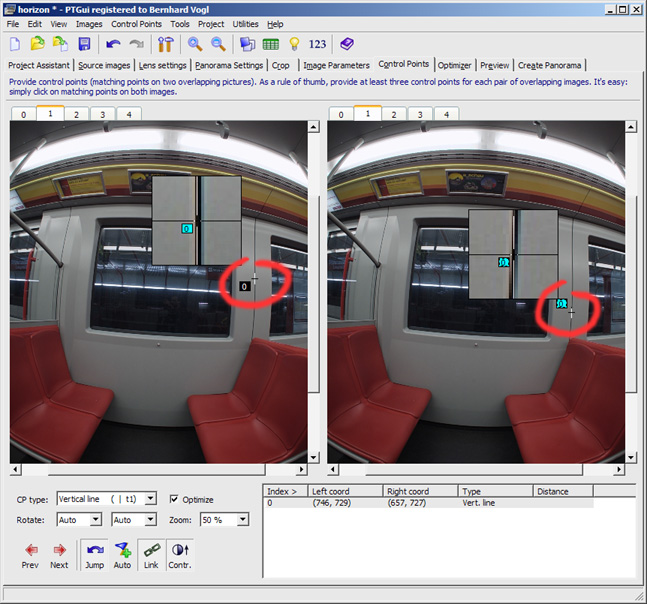
  You may argue that this doesn't seem to be very exact. Basically you are right, but this method is still more exact than aligning the panorama by hand and it also has the advantage to be repeat- and correctable as often as you want.
   

• The Finale: Optimizing and analyzing the optimizer result:

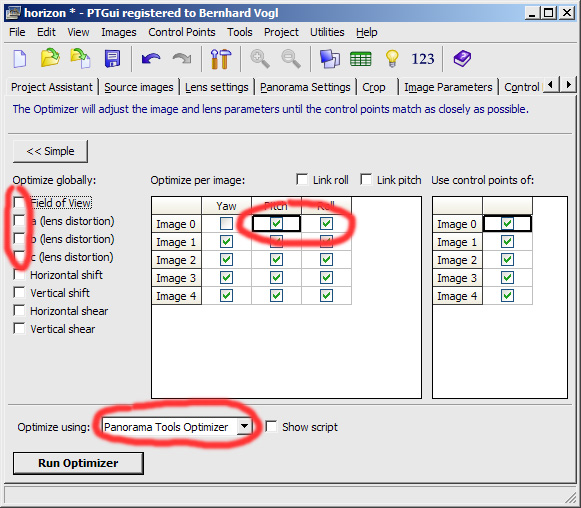
  First of all we have to allow free movement and rotation of all images. We will only prohibit the movement of an anchor image in X-direction. For not falsifying the result, we will deactivate all lens optimizations.
  Furthermore, we have to use the "Panorama Tools Optimizer" instead of PTGui's optimizer.
  In the following image, all needed modifications are marked red:
  

  Now we can run the Optimizer and hopefully, the result will be good:
  

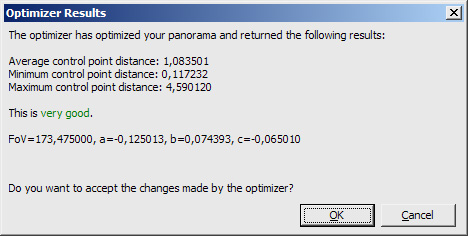
  If you notice a degradation of your Optimizer result, you can use the "Control Point Table" to find the problem:
  
  You can see that the distances of the vertical control points only denote their deviation from a perfect vertical - not their distance from each other (as normal control points would do).
  In our case, we already have a good result. The control points show only low distances.